Exercício de Matemática (Questões ITA 2022) com Gabarito

MATEMÁTICA

ITA 2022 - QUESTÃO 41

Se x = 9 1og120 2 + 3 1og120 3 + 2 log14400 125 podemos afirmar que

a) x = 2.

b) x = 3.

c) x = 4.

d) x = 5.

e) x = 6.

GABARITO.

ITA 2022 - QUESTÃO 42

Considere um triângulo de vértices A, B e C, retângulo em B. Seja r a reta determinada por A e C e seja O um ponto equidistante de A e C no mesmo lado que B com respeito a r.

Sabendo que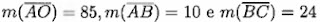

temos que a distância de O a r é

a) 64.

b) 66.

c) 74.

d) 76.

e) 84.

GABARITO.

ITA 2022 - QUESTÃO 43

Seja m ∈ R. Considere os sistemas lineares

Assinale a alternativa correta:

a) Não existe m ∈ R tal que S1 é equivalente a S2.

b) Existe exatamente um m > 0 tal que S1 é equivalente a S2.

c) Existe exatamente um m < 0 tal que S1 é equivalente a S2.

d) Existem exatamente dois valores distintos de m tais que S1 é equivalente a S2.

e) Existem infinitos valores distintos para m tais que S1 é equivalente a S2.

GABARITO.

ITA 2022 - QUESTÃO 44

Sejam z1, z2 ∈ R com z2 ≠ 0. Considere as afirmações:

I. Se z1 + z2 ∈ R e z1 – z2 ∈ R então z1 ∈ R e z2 ∈ R.

II. Se z1 . z2 ∈ R e z1/z2 ∈ R então z1 ∈ R e z2 ∈ R.

III. Se z1 + z2 ∈ R e z1 . z2 ∈ R então z1 ∈ R e z2 ∈ R.

É (são) sempre verdadeira(s):

a) apenas I.

b) I e II.

c) apenas I e III.

d) apenas II.

e) apenas III.

GABARITO.

ITA 2022 - QUESTÃO 45

Considere o polinômio p(z) = z⁴ – 6z³ + 14z² – 6z + 13 e note que p(i) = 0. Considere no plano complexo o quadrilátero cujos vértices são as raízes de p(z).

Podemos afirmar a área desse quadrilátero é

a) 4.

b) 6.

c) 8.

d) 9.

e) 10.

GABARITO.

ITA 2022 - QUESTÃO 46

Seja n ≥ 2 e A, B ∈ Mn(R). Considere as seguintes afirmações:

I. Se AB ≠ BA então ou A ou B não é inversível.

II. Se AB = 0 então BA = 0.

III. Se Aᵀ = –A² e A é inversível então det(A) = –1.

É (são) verdadeira(s):

a) apenas I.

b) apenas II.

c) apenas III.

d) apenas I e III.

e) Nenhuma das afirmações.

GABARITO.

ITA 2022 - QUESTÃO 47

Sejam x, r ∈ R e suponha que –π/2 < x – r ≤ x + r < π/2.

Sobre tan(x–r), tan(x) e tan(x + r), nesta ordem, podemos afirmar que:

a) Nunca determina uma progressão aritmética.

b) Pode determinar uma progressão aritmética apenas se r = 0.

c) Pode determinar uma progressão aritmética apenas se r = 0 ou se r = √3/3

d) Pode determinar uma progressão aritmética para infinitos valores distintos de r.

e) Determina uma progressão aritmética para todo x e r como no enunciado.

GABARITO.

ITA 2022 - QUESTÃO 48

Seja b ∈ R tal que a equação x² – 6bx – (1 – b²)(y² – 2by) + b⁴ + 8b² – 1 = 0 determina uma hipérbole.

Com respeito ao centro C desta hipérbole podemos afirmar:

a) C ∈ {(x, y) ∈ R² / x2/9 + y²/12 < 1}.

b) C ∈ {(x, y) ∈ R² / x2/4 + y²/ 2 > l}.

c) C ∈ {(x, y) ∈ R² / x2/9 – y²/2 < 1}.

d) C ∈ {(z, y) ∈ R² / 3x2– 2y²> 1}.

e) Nenhuma das alternativas anteriores.

GABARITO.

ITA 2022 - QUESTÃO 49

Seja P uma pirâmide regular cujo vértice V é um dos vértices de um cubo de lado l e cuja base é o hexágono formado pelos pontos médios das seis arestas do cubo que não contém V nem o vértice oposto a V.

O raio da esfera que circunscreve P é

a) l√2/12.

b) l√3/12.

c) 5l√2/12.

d) 5l√3/12.

e) l√3/6.

GABARITO.

ITA 2022 - QUESTÃO 50

Considere as seguintes afirmações:

I. Se α e β são planos paralelos distintos e r é urna reta tal que r ∩ α ≠ ∅ então r ∩ β ≠ ∅.

II. Se r é urna reta e P e Q são pontos distintos, então existem infinitos planos equidistantes de P e Q que contêm r.

III. Dado quatro pontos no espaço, existe um único ponto equidistante a eles.

É (são) verdadeira(s):

a) Nenhuma das afirmações.

b) apenas I.

c) apenas II.

d) apenas III.

e) I, II e III.

GABARITO.

ITA 2022 - QUESTÃO 51

Dizemos que a representação binária de um número N ∈ N da forma N = g . 2⁰ + f . 2¹ + e . 2² + d . 2³ + c . 2⁴ + b . 2⁵ + a . 2⁶ é (abcdefg)2, onde a, b, c, d, e, f, g ∈ {0, 1} e omitem-se os algarismos 0 até o primeiro algarismo 1 da esquerda para a direita. Seja k um número inteiro tal que 1 ≤ k ≤ 100.

Qual a probabilidade de k e k + 1 terem representações binárias com um número distinto de algarismos?

a) 2%.

b) 4%.

c) 6%.

d) 8%.

e) 10%.

GABARITO.

ITA 2022 - QUESTÃO 52

Seja A o conjunto de todas as retas que passam por dois vértices distintos de um cubo C. Escolhendo aleatoriamente duas retas distintas de A, a probabilidade dessas retas se interceptarem em um vértice de C é:

a) 4/9.

b) 1/2.

c) 2/3.

d) 1/14.

e) 3/7.

GABARITO.

ITA 2022 - QUESTÃO 53

Sejam α, β e θ ángulos internos de um triângulo. Se cos (β + θ) ≤ cos (α + 2β), podemos afirmar que:

a) O triângulo não é isóceles.

b) O triângulo não é retângulo.

c) O triângulo não é actuângulo.

d) O triângulo não é obtusângulo.