Os nove pontos da figura estão igualmente espaçados na circunferência. Maria quer pintar alguns desses pontos de tal forma que não exista triângulo equilátero cujos vértices estejam todos pintados

OBMEP 2022 - QUESTÃO 14 Os nove pontos da figura estão igualmente espaçados na circunferência. Maria quer pintar alguns desses pontos de tal...

OBMEP 2022 - QUESTÃO 14

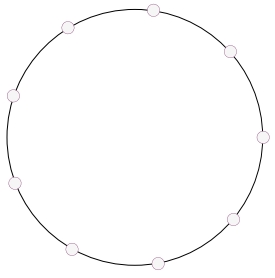
Os nove pontos da figura estão igualmente espaçados na circunferência. Maria quer pintar alguns desses pontos de tal forma que não exista triângulo equilátero cujos vértices estejam todos pintados. Qual é o maior número de pontos que ela pode pintar?

(A) 4

(B) 5

(C) 6

(D 7

(E) 8

QUESTÃO ANTERIOR:

- A figura mostra três circunferências de centros O, P e Q, cada uma tangente às outras nos pontos A, B e C, como indicado

GABARITO:

(C) 6

RESOLUÇÃO:

É possível inscrever três, e apenas três, triângulos equiláteros em um eneágono regular (polígono de nove lados cujos vértices estão igualmente espaçados em uma circunferência), como mostra a figura.

Se pintarmos sete vértices do eneágono, necessariamente um dos triângulos terá os três vértices da mesma cor, pois, se cada triângulo equilátero tiver, no máximo, dois vértices pintados, o total de vértices pintados no eneágono será, no máximo, seis.

Note que podemos pintar seis vértices do eneágono de tal forma que nenhum triângulo tenha os três vértices da mesma cor; por exemplo, pintando A, D, C, F E e H.

Assim, o maior número de pontos que podem ser pintados de tal forma que não exista um triângulo equilátero cujos vértices estejam todos pintados é 6.

OBMEP 2022 - QUESTÃO 15

DISPONÍVEL NA PROVA NÍVEL 2.

PRÓXIMA QUESTÃO:

- A figura abaixo mostra um tabuleiro 5 x 5 formado por 25 quadrados pretos ou brancos. Observe que esse tabuleiro não se altera quando girado de 90º

QUESTÃO DISPONÍVEL EM:

- Provas OBMEP 2022 com Gabarito e Resolução