OBMEP 2021: Os números de 1 a 9 são distribuídos ao acaso e sem repetição nas casas do quadriculado desenhado na lousa ao lado. a) Qual é a ...
OBMEP 2021: Os números de 1 a 9 são distribuídos ao acaso e sem repetição nas casas do quadriculado desenhado na lousa ao lado.
a) Qual é a probabilidade de que a casa central seja preenchida com um número ímpar?
b) Qual é a probabilidade de que o quadriculado tenha uma coluna preenchida apenas com números pares?
c) Qual é a probabilidade de que o quadriculado tenha uma linha e uma coluna preenchidas apenas com números ímpares?
QUESTÃO ANTERIOR:
RESOLUÇÃO:
Observamos inicialmente que podemos considerar o quadriculado fixo na posição apresentada.
Item A
Qualquer casa do tabuleiro (em particular, a casa central) pode ser preenchida de nove maneiras, sendo quatro delas por um número par; a probabilidade pedida é, então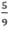 
.
.Item B
A probabilidade de que três casas fixas (não necessariamente na mesma coluna) sejam preenchidas apenas por números pares é 
De fato, a probabilidade de a primeira casa ser preenchida com um número par é de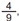 
conforme o item anterior; uma vez preenchida a primeira das três casas com um número par, a probabilidade de a segunda casa ser preenchida com um número par é 
conforme o item anterior; uma vez preenchida a primeira das três casas com um número par, a probabilidade de a segunda casa ser preenchida com um número par é Finalmente, uma vez preenchidas a primeira e a segunda casas com números pares, a probabilidade de a terceira casa também ser preenchida com um número par é 
e segue nossa afirmativa inicial. Como podemos escolher uma coluna de três maneiras, a probabilidade procurada é 
e segue nossa afirmativa inicial. Como podemos escolher uma coluna de três maneiras, a probabilidade procurada é Alternativamente, quatro casas fixas (em particular, uma coluna e uma casa extra) podem ser preenchidas com números pares de 4! maneiras e, após isso, as cinco casas restantes podem ser preenchidas com números ímpares de 5! maneiras. Logo, o número de maneiras de preencher o quadriculado de modo que essas quatro casas tenham números pares é 4! × 5!.
Como o número de maneiras de preencher o quadriculado sem restrições é 9!, a probabilidade de que essas quatro casas sejam preenchidas com números pares é 
Finalmente, podemos fixar uma coluna e uma casa extra de 3 × 6 = 18 maneiras, e segue que a probabilidade procurada é 
Item C
A probabilidade de que cinco casas fixas (não necessariamente formando uma linha e uma coluna) sejam preenchidas por números ímpares é, analogamente ao item anterior, igual a 
Podemos escolher uma linha e uma coluna de 3 × 3 = 9 maneiras diferentes, e segue que a probabilidade pedida é 
.
.Alternativamente, cinco casas fixas (em particular, uma linha e uma coluna) podem ser preenchidas com números ímpares de 5! maneiras e as quatro casas restantes podem ser preenchidas com números pares de 4! maneiras. Podemos fixar uma linha e uma coluna de 3 × 3 = 9 maneiras, e segue, como no item anterior, que a probabilidade pedida é 
Notamos que o fato de a probabilidade em (c) ser a metade daquela em (b) não é apenas uma coincidência numérica, mas decorre do fato de que é possível associar a cada preenchimento do tabuleiro, como em (c), dois preenchimentos distintos, como em (b); reciprocamente, os preenchimentos como em (b) podem ser divididos em grupos de dois, de modo a gerar um preenchimento como em (c). Essa ideia está ilustrada na figura abaixo.
Dessa maneira, outra solução para essa questão é mostrar primeiro (b) e depois usar o argumento acima para mostrar (c), ou vice-versa.
PRÓXIMA QUESTÃO:
QUESTÃO DISPONÍVEL EM:
