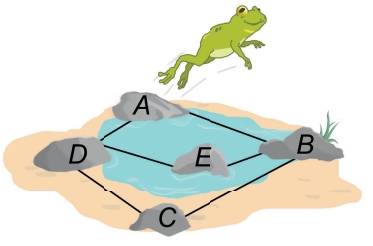
OBMEP 2021: Cinco pedras, A, B, C, D e E, estão dispostas como na figura. Kiko, o sapo simpático, pula de uma pedra para outra somente se el...
OBMEP 2021: Cinco pedras, A, B, C, D e E, estão dispostas como na figura. Kiko, o sapo simpático, pula de uma pedra para outra somente se elas estiverem ligadas por um segmento. Assim, ele pode pular, partindo de A, para B ou D, mas não para E ou C. Por exemplo, começando em A e terminando em D, ele pode realizar o seguinte passeio de 5 pulos: A → B → E → D → C → D.
a) Quantos são os passeios de três pulos que Kiko pode fazer começando em A e terminando em B?
b) Kiko quer fazer um passeio de 1001 pulos, começando em A. Em quais pedras ele poderá terminar esse passeio? Justifi que sua resposta.
c) Quantos são os passeios de 2020 pulos que Kiko pode fazer começando em A e terminando em C?
QUESTÃO ANTERIOR:
RESOLUÇÃO:
Item A
No primeiro pulo, Kiko tem duas opções: ele pode ir de A para B ou para D. No segundo pulo, Kiko tem três opções, tanto partindo de B quanto partindo de D. Note que, após esse segundo pulo, Kiko estará, necessariamente, em A, E ou C. No pulo final, de qualquer uma dessas pedras, ele tem apenas uma opção para ir para B. Assim, pelo princípio multiplicativo, Kiko pode realizar 2 × 3 × 1 = 6 passeios distintos, começando em A e terminando em B.
Podemos listar os passeios, explicitamente, também: A→B→A→B, A→B→E→B,A→B→C→B,A→D→A→B, A→D→E→B, A→D→C→B.
Item B
Analisando-se alguns casos com poucos pulos, como no item anterior, emerge um padrão: em um passeio qualquer, logo após os pulos de número ímpar (primeiro, terceiro, quinto e assim por diante), Kiko estará em B ou D, e, logo após os pulos de número par (segundo, quarto, sexto e assim por diante), Kiko estará em A, E ou C.
Isso pode ser entendido da seguinte maneira: se pintarmos as pedras B e D de branco e as pedras A, E e C de preto, vemos que de uma pedra branca ele pula para uma preta, e de uma pedra preta ele pula para uma branca.
A figura ao lado ilustra essa ideia.
Isso indica que, após o 1001º pulo, Kiko irá se encontrar, necessariamente, em B ou D. Note que o argumento não basta para mostrar que, de fato, ele pode terminar tanto em B quanto em D. Para isso, devemos mostrar que é possível, após o 1001º pulo, terminar em qualquer uma das duas pedras.
Uma maneira de mostrar que as duas pedras são finais possíveis para o passeio de Kiko é exibir, explicitamente, passeios que terminam em B ou em D depois de 1001 pulos. Um passeio assim pode ser feito da seguinte maneira: simplesmente Kiko pula de A para B e de B para A até completar 1000 pulos. Após o milésimo pulo ele estará em A. De A ele pode dar mais um pulo, tanto para B quanto para D.
Item C
Como discutido no item anterior, Kiko tem duas opções para o primeiro pulo (B ou D), 3 opções para o segundo pulo (A, C ou E), e assim por diante, até o 2019º pulo, quando tem duas opções. No 2020º pulo, Kiko tem apenas uma opção, que é pular para C. Assim, pelo princípio multiplicativo, Kiko pode realizar 2 × 3 × 2 × 3 × … × 2 × 1 = 2¹⁰¹⁰ × 3¹⁰⁰⁹ passeios.
PRÓXIMA QUESTÃO:
QUESTÃO DISPONÍVEL EM: