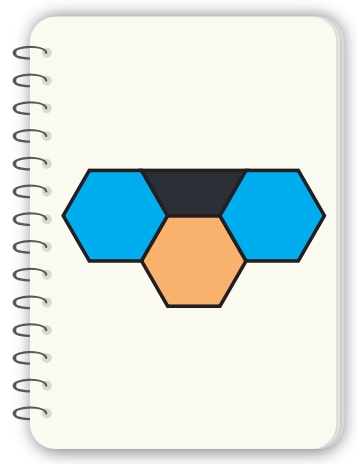
OBMEP 2021: Maria pinta, em seu caderno, figuras formadas por trapézios e hexágonos. Cada hexágono pode ser pintado de azul, bege ou cinza, ...
OBMEP 2021: Maria pinta, em seu caderno, figuras formadas por trapézios e hexágonos. Cada hexágono pode ser pintado de azul, bege ou cinza, e cada trapézio, de azul ou preto. Polígonos com um lado em comum não podem ter a mesma cor. A figura ao lado é um exemplo de uma pintura feita por Maria.
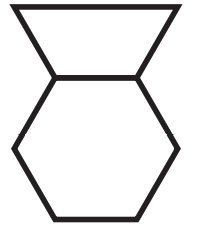
a) De quantas maneiras Maria pode pintar a figura abaixo?
b) De quantas maneiras Maria pode pintar a figura abaixo?
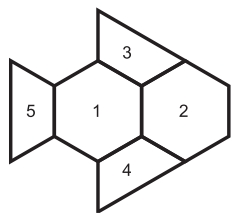
c) De quantas maneiras Maria pode pintar a figura abaixo
QUESTÃO ANTERIOR:
RESOLUÇÃO:
Item A
Maria pode pintar de azul tanto o hexágono como o trapézio e, portanto, essa cor deve ser tratada separadamente.
Caso 1: se o hexágono for pintado de azul, então, para não repetir a mesma cor no trapézio, este só pode ser pintado de preto (1 possibilidade).
Caso 2: se o hexágono não for pintado de azul (2 possibilidades), Maria poderá pintar o trapézio de azul ou de preto (2 possibilidades). Pelo princípio multiplicativo da contagem, há, então, 2 × 2 = 4 possibilidades de pinturas.
Juntando os dois casos, vemos que Maria pode pintar a Figura 1 de 1 + 4 = 5 maneiras diferentes.
Item B
Novamente, façamos a divisão em casos.
Caso 1: se o hexágono for pintado de azul por Maria, todos os três trapézios devem ser pintados de preto (1 possibilidade).
Caso 2: se o hexágono não for pintado de azul (2 possibilidades), cada um dos três trapézios da Figura 2 pode ser pintado de azul ou preto. Pelo princípio multiplicativo, há 2 × 2 × 2 × 2 = 16 possibilidades de pinturas.
Juntando os dois casos, vemos que Maria pode pintar a Figura 2 de 1 + 16 = 17 maneiras diferentes.
Item C
Vamos enumerar as regiões de acordo com a figura ao lado:
Vamos dividir em 6 casos:
• Hexágono 1 na cor azul, hexágono 2 na cor bege. Nesse caso, os trapézios 3, 4 e 5 devem ser pintados de preto (1 possibilidade).
• Hexágono 1 na cor azul, hexágono 2 na cor cinza. Nesse caso, também os trapézios 3, 4 e 5 devem ser pintados de preto (1 possibilidade).
• Hexágono 1 na cor bege, hexágono 2 na cor azul. Nesse caso, os trapézios 3 e 4 devem ser pintados de preto, mas o trapézio 5 pode ser pintado de azul ou preto (2 possibilidades).
• Hexágono 1 na cor bege, hexágono 2 na cor cinza. Cada trapézio pode ser pintado de duas cores (2 × 2 × 2 = 8 possibilidades).
• Hexágono 1 na cor cinza, hexágono 2 na cor azul. Nesse caso, os trapézios 3 e 4 devem ser pintados de preto e o trapézio 5 pode ser pintado de duas cores (2 possibilidades).
• Hexágono 1 na cor cinza, hexágono 2 na cor bege. Cada trapézio pode ser pintado de duas cores (2 × 2 × 2 = 8 possibilidades).
Logo, há 1 + 1 + 2 + 8 + 2 + 8 = 22 maneiras diferentes de Maria pintar a Figura 3.
PRÓXIMA QUESTÃO:
QUESTÃO DISPONÍVEL EM: