OBMEP 2021: Joãozinho fez todas as divisões possíveis com dois números diferentes pertencentes ao conjunto {1, 2, 3, 4, 5, 6, 7, 8, 9}

OBMEP 2021: Joãozinho fez todas as divisões possíveis com dois números diferentes pertencentes ao conjunto {1, 2, 3, 4, 5, 6, 7, 8, 9}. Por ...

OBMEP 2021: Joãozinho fez todas as divisões possíveis com dois números diferentes pertencentes ao conjunto {1, 2, 3, 4, 5, 6, 7, 8, 9}. Por exemplo, com os números 2 e 5, ele fez as seguintes divisões:  (obteve como resultado 0,4) e  (obteve como resultado 2,5).

a) Em quantas divisões Joãozinho obteve como resultado um número inteiro?

b) Em quantas divisões Joãozinho obteve como resultado um número maior do que 0,5?

c) Quantos resultados diferentes foram obtidos por Joãozinho?

QUESTÃO ANTERIOR:

- OBMEP 2021: Janaína desenha quadrados formados por quadrados menores, cujos lados têm medidas inteiras.

RESOLUÇÃO:

Uma solução:

Item A

Os números inteiros nas divisões que Joãozinho fez são aqueles em que o dividendo é múltiplo do divisor, ou seja: divisões 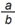 em que a é múltiplo de b. Como a e b são dois números diferentes do conjunto {1, 2, 3, 4, 5, 6, 7, 8, 9}, para cada possibilidade de divisor b em {1, 2, 3, 4, 5, 6, 7, 8, 9}, devemos contar as possibilidades de dividendo a em {1, 2, 3, 4, 5, 6, 7, 8, 9}, tais que a seja múltiplo de b e diferente de b. Temos:

• para b = 1 as possibilidades para a são {2, 3, 4, 5, 6, 7, 8, 9}, ou seja, 8 possibilidades;

• para b = 2 as possibilidades para a são {4, 6, 8}, ou seja, 3 possibilidades;

• para b = 3 as possibilidades para a são {6, 9}, ou seja, 2 possibilidades;

• para b = 4 a possibilidade para a é {8}, ou seja, 1 possibilidade;

• para b = 5, 6, 7, 8, 9 não existem possibilidades para a.

Logo, Joãozinho obteve como resultado um número inteiro em 8 + 3 + 2 + 1 = 14 divisões.

Item B

Os números maiores do que 0,5 nas divisões que Joãozinho fez são aqueles em que o dividendo é maior do que a metade do divisor, ou seja: divisões 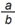   em que a é maior do que a metade de b. Como a e b são dois números diferentes do conjunto {1, 2, 3, 4, 5, 6, 7, 8, 9}, para cada possibilidade de divisor b em {1, 2, 3, 4, 5, 6, 7, 8, 9}, devemos contar as possibilidades de dividendo a em {1, 2, 3, 4, 5, 6, 7, 8, 9} tais que a seja diferente de b e maior do que a metade de b. Temos:

• para b = 1 as possibilidades para a são {2, 3, 4, 5, 6, 7, 8, 9}, ou seja, 8 possibilidades;

• para b = 2 as possibilidades para a são {3, 4, 5, 6, 7, 8, 9}, ou seja, 7 possibilidades;

• para b = 3 as possibilidades para a são {2, 4, 5, 6, 7, 8, 9}, ou seja, 7 possibilidades;

• para b = 4 as possibilidades para a são {3, 5, 6, 7, 8, 9}, ou seja, 6 possibilidades;

• para b = 5 as possibilidades para a são {3, 4, 6, 7, 8, 9}, ou seja, 6 possibilidades;

• para b = 6 as possibilidades para a são {4, 5, 7, 8, 9}, ou seja, 5 possibilidades;

• para b = 7 as possibilidades para a são {4, 5, 6, 8, 9}, ou seja, 5 possibilidades;

• para b = 8 as possibilidades para a são {5, 6, 7, 9}, ou seja, 4 possibilidades;

• para b = 9 as possibilidades para a são {5, 6, 7, 8}, ou seja, 4 possibilidades.

Logo, Joãozinho obteve como resultado um número maior do que 0,5 em 8 + 7 + 7 + 6 + 6 + 5 + 5 + 4 + 4 = 52 divisões.

Item C

Os resultados diferentes nas divisões que Joãozinho fez são aqueles em que o dividendo e o divisor não possuem fatores comuns, ou seja: divisões 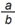     em que a e b são primos entre si, pois, se houver um fator comum k a a e b, então a = k × a’ e b = k × b’, e esse fator comum k pode ser cancelado na divisão  e a nova divisão 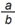     também será uma divisão feita por Joãozinho. Como a e b são dois números diferentes do conjunto {1, 2, 3, 4, 5, 6, 7, 8, 9}, para cada possibilidade de divisor b em {1, 2, 3, 4, 5, 6, 7, 8, 9}, devemos contar as possibilidades de dividendo a em {1, 2, 3, 4, 5, 6, 7, 8, 9} tais que a e b sejam primos entre si. 

Temos:

• para b = 1 as possibilidades para a são {2, 3, 4, 5, 6, 7, 8, 9}, ou seja, 8 possibilidades;

• para b = 2 as possibilidades para a são {1, 3, 5, 7, 9}, ou seja, 5 possibilidades;

• para b = 3 as possibilidades para a são {1, 2, 4, 5, 7, 8}, ou seja, 6 possibilidades;

• para b = 4 as possibilidades para a são {1, 3, 5, 7, 9}, ou seja, 5 possibilidades;

• para b = 5 as possibilidades para a são {1, 2, 3, 4, 6, 7, 8, 9}, ou seja, 8 possibilidades;

• para b = 6 as possibilidades para a são {1, 5, 7}, ou seja, 3 possibilidades;

• para b = 7 as possibilidades para a são {1, 2, 3, 4, 5, 6, 8, 9}, ou seja, 8 possibilidades;

• para b = 8 as possibilidades para a são {1, 3, 5, 7, 9}, ou seja, 5 possibilidades;

• para b = 9 as possibilidades para a são {1, 2, 4, 5, 7, 8}, ou seja, 6 possibilidades.

Logo, Joãozinho obteve 8 + 5 + 6 + 5 + 8 + 3 + 8 + 5 + 6 = 54 resultados diferentes nas suas divisões.

Outra solução:

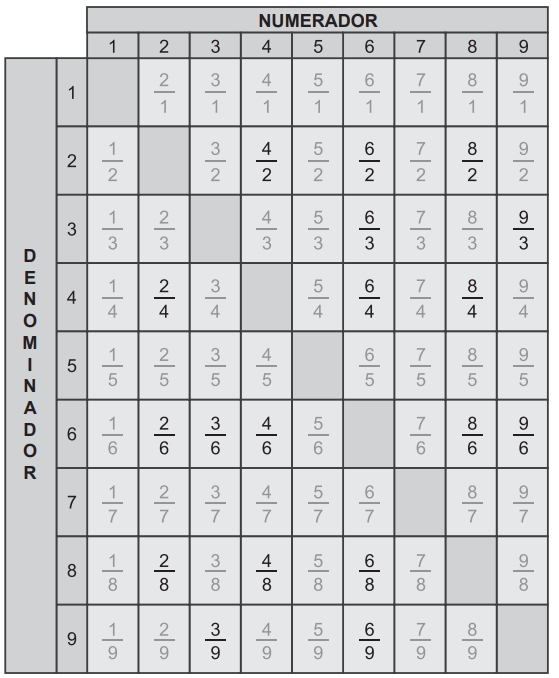
Como Joãozinho fez todas as divisões possíveis com dois números diferentes do conjunto {1, 2, 3, 4, 5, 6, 7, 8, 9}, no total ele fez 9 × 8 = 72 divisões, conforme mostra a tabela ao lado.

Item A

Joãozinho obteve como resultado um número inteiro nas divisões em que o numerador é um múltiplo do denominador, ou seja:

• nas oito divisões em que o denominador é igual a um:

 

• em três divisões em que o denominador é igual a dois:

• em duas divisões em que o denominador é igual a três:

• em uma divisão em que o denominador é igual a quatro:

Logo, Joãozinho obteve como resultado um número inteiro em 14 divisões.

Item B

Joãozinho obteve como resultado um número maior do que 0,5 nas divisões em que o numerador é maior do que a metade do denominador, ou seja:

• nas oito divisões em que o denominador é igual a um:

• em sete divisões em que o denominador é igual a dois:

• em sete divisões em que o denominador é igual a três:

• em seis divisões em que o denominador é igual a quatro:

• em seis divisões em que o denominador é igual a cinco:

• em cinco divisões em que o denominador é igual a seis:

• em cinco divisões em que o denominador é igual a sete:

• em quatro divisões em que o denominador é igual a oito:

• em quatro divisões em que o denominador é igual a nove:

Logo, Joãozinho obteve como resultado um número maior do que 0,5 em 8 + 7 + 7 + 6 + 6 + 5 + 5 + 4 + 4 = 52 divisões.

Item C

Para saber quantos resultados diferentes Joãozinho, obteve é preciso contar as divisões que não podem ser simplificadas, ou seja, aquelas em que o numerador e o denominador são primos entre si, ou seja:

• oito em que o denominador é igual a um: 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9; 

• cinco em que o denominador é igual a dois:

• seis em que o denominador é igual a três:

• cinco em que o denominador é igual a quatro:

• oito em que o denominador é igual a cinco:

• três em que o denominador é igual a seis:

• oito em que o denominador é igual a sete:

• cinco em que o denominador é igual a oito:

• seis em que o denominador é igual a nove:

Logo, Joãozinho obteve 8 + 5 + 6 + 5 + 8 + 3 + 8 + 5 + 6 = 54 resultados diferentes.

Outra maneira de contar os resultados diferentes que Joãozinho obteve é retirar das 72 divisões que ele fez aquelas em que o numerador e o denominador são ambos múltiplos de 2, 3, 5 ou 7. Como os numeradores e denominadores são números diferentes do conjunto {1, 2, 3, 4, 5, 6, 7, 8, 9}, temos:

• numerador e denominador ambos múltiplos de 2: 

• 4 possibilidades para um (2, 4, 6 ou 8) e 3 possibilidades (a deve ser diferente de b) para outro: 4 × 3 = 12

• numerador e denominador ambos múltiplos de 3: 

• 3 possibilidades para um (3, 6, 9) e 2 possibilidades (a deve ser diferente de b) para outro: 3 × 2 = 6

• numerador e denominador ambos múltiplos de 5: 

• 1 possibilidade para um (somente o 5) e 0 possibilidade para outro: 1 × 0 = 0

• numerador e denominador ambos múltiplos de 7: 

• 1 possibilidade para um (somente o 7) e 0 possibilidade para outro: 1 × 0 = 0

Logo, Joãozinho obteve 72 − 12 − 6 = 54 resultados diferentes. Esses 54 números aparecem em cinza na tabela anterior.

PRÓXIMA QUESTÃO:

- OBMEP 2021: Maria pinta, em seu caderno, figuras formadas por trapézios e hexágonos.

QUESTÃO DISPONÍVEL EM:

- Provas OBMEP 2021 com Gabarito e Resolução