SANTA CASA 2023: Considere que, devido à sua extensão quando comparada com sua espessura

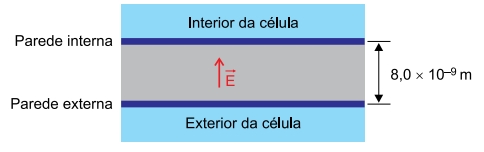
SANTA CASA 2023: Considere que, devido à sua extensão quando comparada com sua espessura, uma membrana celular possa ser aproximada por duas paredes planas, paralelas e eletrizadas com cargas de sinais opostos. Admita que no interior dessa membrana exista um campo elétrico uniforme de intensidade E = 5,0 × 10⁶ V/m, devido às diferentes concentrações iônicas no interior e no exterior da célula.

a) Considere que a distância entre as duas paredes dessa membrana celular seja 8,0 × 10⁻⁹ m, que a direção do campo elétrico seja perpendicular a essas paredes e que seu sentido seja de fora para dentro da célula. Calcule a diferença de potencial, em volts, entre as duas paredes dessa membrana. Em seguida, determine o sinal das cargas elétricas em cada uma dessas paredes. Justifique sua resposta.

b) Suponha que um íon de sódio, com carga elétrica de 1,6 × 10–19 C, possa se mover no interior dessa membrana com velocidade de 1,0 × 10⁻⁴ m/s. Calcule a intensidade da força elétrica, em newtons, que atua sobre esse íon na região entre as paredes dessa membrana. Em seguida, calcule a intensidade mínima do campo magnético, em teslas, que deve ser aplicado sobre a membrana para produzir sobre esse íon uma força magnética de mesma intensidade que a força elétrica que atua sobre ele no interior da membrana.

RESOLUÇÃO:

a) 1) Cálculo da ddp entre as duas paredes.

Temos um campo elétrico uniforme (C.E.U.)

E . d = U

Temos:

E = 5,0 . 10⁶ V/m

d = 8,0 . 10⁻⁹ m

U = (5,0 . 10⁶) . (8,0 . 10⁻⁹) (unid. SI)

U = 40,0 . 10⁻³ V

U = 4,0 . 10⁻² V

2) Determinação dos sinais das cargas