OBMEP 2022 - QUESTÃO 11 Em uma escola foram criados três clubes distintos com 15 alunos cada. Nenhum aluno participa de três clubes, mas os ...
OBMEP 2022 - QUESTÃO 11
Em uma escola foram criados três clubes distintos com 15 alunos cada. Nenhum aluno participa de três clubes, mas os alunos podem participar de mais de um clube. Quantos alunos, no mínimo, participam desses clubes?
(A) 23
(B) 24
(C) 25
(D) 26
(E) 27
QUESTÃO ANTERIOR:
GABARITO:
(A) 23
RESOLUÇÃO:
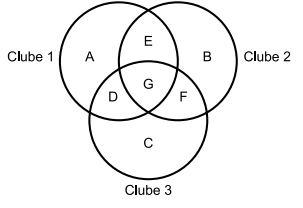
Não temos resolução para essa questão! Você sabe explicar? Copie o link dessa página e envie sua resolução clicando AQUI!Podemos fazer um diagrama de Venn representando essa situação:
As letras A, B, ..., G representam o número de membros naquela região. Por exemplo, a letra A representa o número de membros exclusivos do clube 1, enquanto a letra E representa o número de membros que pertencem exclusivamente aos clubes 1 e 2.
Como nenhum aluno é membro dos três clubes, G = 0.
Queremos minimizar o número total de alunos, mas de tal forma que cada clube tenha exatamente 15 alunos, ou seja,
A+D+E=15
C+D+F=15
B+E+F=15
Somando as três equações, obtemos A + B + C + 2(D + E + F) = 45. Isso mostra que A + B + C não pode ser 0, pois 0 lado direito é ímpar. De forma a minimizar o número de alunos, podemos supor, então, que A = 1, B=0, C=0, sem perda de generalidade.
Como estamos supondo que A = 1, temos D + E + F = 22. O número mínimo de alunos tem que ser, portanto, igual ou maior do que 23. Podemos mostrar explicitamente que é possível satisfazer às condições do problema com 23 alunos no total; basta tomar D= E = 7 e F =8.
PRÓXIMA QUESTÃO:
QUESTÃO DISPONÍVEL EM: