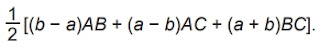OBMEP 2021: Na figura, as circunferências de raios a e b, centradas em O e O’, são tangentes aos lados do ângulo em S e T e em S’ e T’, resp...
OBMEP 2021: Na figura, as circunferências de raios a e b, centradas em O e O’, são tangentes aos lados do ângulo em S e T e em S’ e T’, respectivamente. Elas também tangenciam os lados AB e AC de um triângulo ABC, em que A pertence a TT’ e BC está contido em SS’. Esse triângulo ABC tem altura h relativa à base BC.
a) Calcule o perímetro do triângulo ABC quando SS’ = 10.
b) Denote as áreas dos triângulos ABC, ABO e ACO’ por A1, A2 e A3, respectivamente. Explique por que a área do hexágono OSS’O’T’T é dada por A1 + 2A2 + 2A3.
c) Mostre que a área do triângulo ABC é 
d) Mostre que, se AB = AC, então h = a + b.
QUESTÃO ANTERIOR:
RESOLUÇÃO:
Utilizaremos na solução desse problema o teorema das tangentes, que estabelece que, se duas tangentes são traçadas de um mesmo ponto a uma mesma circunferência, então, os segmentos que unem este ponto até os pontos de tangência são iguais.
Item A
Queremos calcular o perímetro do triângulo ABC quando SS’ = 10.

Somando as equações 1 e 2, obtemos
(BM + AM) + BC + (CN + AN) = 2 SS’ = 20 AB + BC + AC = 2 SS’ = 20.
Assim, o perímetro do triângulo ABC é igual a 20.
Item B
Denote as áreas dos triângulos ABC, ABO e ACO’ por A1, A2 e A3, respectivamente.
Vamos mostrar que a área do hexágono OSS’O’T’T é A1 + 2A2 + 2A3.
Observemos a figura ao lado.
Logo,
Item C
Vamos mostrar agora que a área do triângulo ABC é
OSS’O’ é um trapézio de bases a e b e altura SS’ (do item A,SS’ = 
Por outro lado, área OSS’O’ é igual à metade da área do hexágono OSS’O’T’T; portanto, usando o resultado encontrado no item B,
PRÓXIMA QUESTÃO:
QUESTÃO DISPONÍVEL EM: