Exercício de Matemática (Questões UFRGS 2020) com Gabarito MATEMÁTICA UFRGS 2020 - QUESTÃO 01 O valor de é GABARITO .
Exercício de Matemática (Questões UFRGS 2020) com Gabarito
MATEMÁTICA
UFRGS 2020 - QUESTÃO 01
O valor de 
é
é
GABARITO.
UFRGS 2020 - QUESTÃO 02
Considere as seguintes afirmações sobre números racionais.
Quais estão corretas?
(A) Apenas I.
(B) Apenas II.
(C) Apenas III.
(D) Apenas II e III.
(E) I, II e III.
GABARITO. (A) Apenas I.
UFRGS 2020 - QUESTÃO 03
Se a equação x² + 2x - 8 = 0 tem as raízes a e b, então o valor de 
é
é
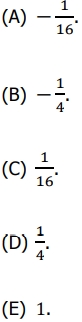
GABARITO.
UFRGS 2020 - QUESTÃO 04
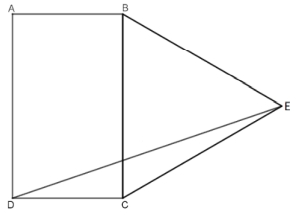
Na figura abaixo, tem-se um retângulo ABCD, de lados 
e 
e um triângulo equilátero BEC, construído sobre o lado 
e e um triângulo equilátero BEC, construído sobre o lado 
A medida de 
é
é
GABARITO.
UFRGS 2020 - QUESTÃO 05
Considere dois círculos de centros A e C, raio 1 e tangentes entre si. O segmento 
é diagonal do quadrado ABCD. Os círculos de centros B e D são tangentes aos círculos de centros A e C, como mostra a figura abaixo.
é diagonal do quadrado ABCD. Os círculos de centros B e D são tangentes aos círculos de centros A e C, como mostra a figura abaixo.
O raio dos círculos de centros B e D é
(A) √2 - 1.
(B) 1.
(C) 2.
(D) √2 + 1.
(E) 2√2.
GABARITO. (A) √2 - 1.
UFRGS 2020 - QUESTÃO 06
Considere o hexágono regular ABCDEF de lado 1. Sobre o lado 
do hexágono, constrói-se o quadrado AGHF, como mostra a figura abaixo. Sendo M o ponto médio de 
, constrói-se o triângulo CDM.
do hexágono, constrói-se o quadrado AGHF, como mostra a figura abaixo. Sendo M o ponto médio de , constrói-se o triângulo CDM.
A área do triângulo CDM é
GABARITO.
UFRGS 2020 - QUESTÃO 07
Considere o cubo ABCDEFGH, representado na figura abaixo, cuja aresta mede 4 e M é o ponto médio da aresta
A área do triângulo MHG é
(A) 2√2.
(B) 4√2.
(C) 8√2.
(D) 16√2.
(E) 32√2.
GABARITO. (C) 8√2.
UFRGS 2020 - QUESTÃO 08
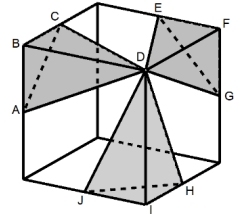
Considere o cubo e os tetraedros ABCD, EFGD e HIJD, nos quais os pontos A, C, E, G, H e J são pontos médios de arestas do cubo, como representado na figura abaixo.
A razão entre a soma dos volumes dos tetraedros ABCD, EFGD e HIJD e o volume do cubo é
GABARITO.
UFRGS 2020 - QUESTÃO 09
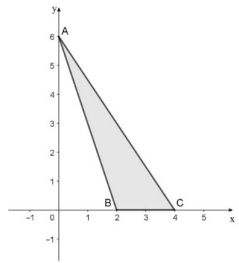
Considere os pontos A, B e C, de coordenadas inteiras, que determinam os vértices do triângulo ABC, representado no sistema de coordenadas cartesianas abaixo.
A revolução do triângulo ABC, em torno do eixo x, gera o sólido P, e a revolução do triângulo ABC, em torno do eixo y, gera o sólido Q.
A razão entre os volumes de P e Q é
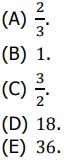
GABARITO. (B) 1.
UFRGS 2020 - QUESTÃO 10
A área da região determinada pela interseção das desigualdades 
e 
é
e é
GABARITO.
UFRGS 2020 - QUESTÃO 11
Considere um retângulo ABCD, de lados 
e 
e um ponto P construído sobre o lado
e e um ponto P construído sobre o lado
. Traçando a reta r perpendicular ao lado que passa pelo ponto P, determina-se o polígono ADEF, em que E e F são pontos de interseção de r com os segmentos 
e 
respectivamente, como mostra a figura abaixo.
Tomando x como a medida do segmento 
a função A(x) que expressa a área de ADEF em função de x, entre as alternativas abaixo, é
a função A(x) que expressa a área de ADEF em função de x, entre as alternativas abaixo, é
GABARITO.
UFRGS 2020 - QUESTÃO 12
Considere as funções f(x) = |x + 1| e 𝑔(x) = -|x| - 1.
O intervalo tal que f(x) > 𝑔(x) é
GABARITO. (E) (-∞, +∞)
UFRGS 2020 - QUESTÃO 13
A concentração de alguns medicamentos no organismo está relacionada com a meia-vida, ou seja, o tempo necessário para que a quantidade inicial do medicamento no organismo seja reduzida pela metade.
Considere que a meia-vida de determinado medicamento é de 6 horas. Sabendo que um paciente ingeriu 120 mg desse medicamento às 10 horas, assinale a alternativa que representa a melhor aproximação para a concentração desse medicamento, no organismo desse paciente, às 16 horas do dia seguinte.
(A) 2,75 mg.
(B) 3 mg.
(C) 3,75 mg.
(D) 4 mg.
(E) 4,25 mg.
GABARITO. (C) 3,75 mg.
UFRGS 2020 - QUESTÃO 14
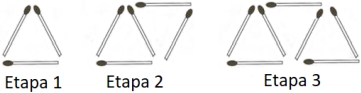
Considere o padrão de construção de triângulos com palitos, representado nas figuras abaixo.
Na etapa n, serão utilizados 245 palitos. Nessas condições, n é igual a
(A) 120.
(B) 121.
(C) 122.
(D) 123.
(E) 124.
GABARITO. (C) 122.
UFRGS 2020 - QUESTÃO 15
A figura a seguir é formada por quadrados de lados 
e assim sucessivamente.
e assim sucessivamente.A construção é tal que os pontos P1, P2, P3, ..., B são colineares, e as bases dos quadrados têm medida 
e assim por diante. O ponto A é vértice do quadrado de lado 
como representado na figura abaixo.
e assim por diante. O ponto A é vértice do quadrado de lado como representado na figura abaixo.
A medida do segmento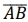 
é
é(A) 1.
(B) √2.
(C) √3.
(D) 2.
(E) √5.
GABARITO. (E) √5.
UFRGS 2020 - QUESTÃO 16
Se log 2 = x e log 3 = y, então log 288 é
(A) 2x + 5y.
(B) 5x + 2y.
(C) 10xy.
(D) x² + y².
(E) x² - y².
GABARITO. (B) 5x + 2y.
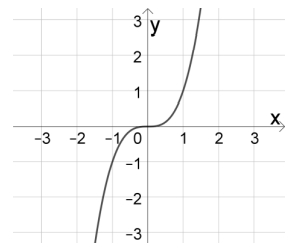
UFRGS 2020 - QUESTÃO 17
O gráfico de f(x) = x³ está representado na imagem a seguir.
O esboço do gráfico de g(x) = x³ + 3x² + 3x + 1 está representado na alternativa
GABARITO.
UFRGS 2020 - QUESTÃO 18
O valor máximo da função trigonométrica f(x) = √2sen(x) + √2cos(x) é
(A) √2.
(B) 2.
(C) 3.
(D) √5.
(E) π.
GABARITO. (B) 2.
UFRGS 2020 - QUESTÃO 19
Considere dois círculos tangentes entre si, de centros A e B sobre a reta r, e tais que o raio de cada um tenha medida 10.
Os segmentos 
e 
são tangentes aos círculos e têm extremidades nos pontos de tangência C, D, E e F, como representado na figura a seguir.
e são tangentes aos círculos e têm extremidades nos pontos de tangência C, D, E e F, como representado na figura a seguir.
A área da região sombreada é
(A) 100 - 25π.
(B) 200 - 50π.
(C) 200 + 50π.
(D) 400 - 100π.
(E) 400 + 100π.
GABARITO. (D) 400 - 100π.
UFRGS 2020 - QUESTÃO 20
A área do quadrilátero formado pelos pontos de interseção da circunferência de equação (x + 1)² + y² = 4 com os eixos coordenados é
(A) √3.
(B) 2√3.
(C) 3√3.
(D) 4√3.
(E) 12.
GABARITO. (D) 4√3.
UFRGS 2020 - QUESTÃO 21
Para que o sistema de equações lineares 
seja possível e determinado, é necessário e suficiente que
seja possível e determinado, é necessário e suficiente que(A) α ∈ R.
(B) α = 2.
(C) α = 1.
(D) α ≠ 1.
(E) α ≠ 2.
GABARITO. (E) α ≠ 2.
UFRGS 2020 - QUESTÃO 22
Um aplicativo de transporte disponibiliza em sua plataforma a visualização de um mapa com ruas horizontais e verticais que permitem realizar deslocamentos partindo do ponto A e chegando ao ponto B, conforme representado na figura abaixo.
O número de menores caminhos possíveis que partem de A e chegam a B, passando por C, é
(A) 28.
(B) 35.
(C) 100.
(D) 300.
(E) 792.
GABARITO. (D) 300.
UFRGS 2020 - QUESTÃO 23
Um jogador, ao marcar números em um cartão de aposta, como o representado na figura abaixo, decidiu utilizar apenas seis números primos.
A probabilidade de que os seis números sorteados no cartão premiado sejam todos números primos é
GABARITO.
UFRGS 2020 - QUESTÃO 24
Após a aplicação de uma prova de Matemática, em uma turma de Ensino Médio com 30 estudantes, o professor organizou os resultados, conforme a tabela a seguir.
A nota mediana dessa prova de Matemática é
(A) 6,0.
(B) 7,0.
(C) 8,0.
(D) 9,0.
(E) 9,5.
GABARITO. (B) 7,0.
UFRGS 2020 - QUESTÃO 25
O gráfico abaixo representa a quantidade de dados armazenados no mundo inteiro, em zettabytes.
Fonte: Gráfico adaptado de UNECE Statistics Wikis
(United Nations Economic Commission for Europe).
Com base nos dados do gráfico, considere as afirmações abaixo.
I - Em relação a 2019, a expectativa é que a quantidade de dados armazenados cresça mais de 20% em 2020.
II - De 2017 a 2019, em termos percentuais, a quantidade de dados armazenadoscresceu mais de 100%.
III- Em termos percentuais, pode-se afirmar que a quantidade de dados armazenadoscresceu mais no período de 2012 a 2016 do que no período de 2016 a 2019.
Quais estão corretas?
(A) Apenas I.
(B) Apenas II.
(C) Apenas III.
(D) Apenas I e II.
(E) I, II e III.
GABARITO. (E) I, II e III.
