Exercício de Matemática (Questões UECE 2021.1) com Gabarito QUESTÃO 01 UECE 2021.1: Sejam os conjuntos K = { x ∈ N tais que 0 < x < 1...
Exercício de Matemática (Questões UECE 2021.1) com Gabarito
QUESTÃO 01
UECE 2021.1: Sejam os conjuntos K = { x ∈ N tais que 0 < x < 100 }, X = { x ∈ K e x é múltiplo de 2} , Y = { x ∈ K e x é múltiplo de 3}, Z = { x ∈ K e x é múltiplo de 5}.
Se V = X ∩ Y ∩ Z, então, o número de subconjuntos de V é
A) 8.
B) 16.
C) 12.
D) 20.
GABARITO. A) 8.
QUESTÃO 02
UECE 2021.1: Se o polinômio P(x) = x⁵+x⁴+x³+x³+x+k, onde k é um número real, é divisível por x–1, então, o valor da soma P(2) + P(–2) é
A) 10.
B) 30.
C) 20.
D) 40.
GABARITO. B) 30.
QUESTÃO 03
UECE 2021.1: No conjunto dos números reais positivos, sejam (x1, x2, x3,....) uma progressão geométrica cuja razão é o número real q e (y1, y2, y3,....) uma progressão aritmética cuja razão é r, com yn = 3 e y5 = 7.
Se para cada número inteiro positivo n, tivermos yn = log2(xn), então, é correto afirmar que o valor da soma x1 + q + r é
A) 11.
B) 13.
C) 12.
D) 14.
GABARITO. A) 11.
QUESTÃO 04
UECE 2021.1: Seja f a função real de variável real definida por f(x) = 8aˣ, onde a é um número real positivo diferente de um.
Se f(3) = 125, então, pode-se afirmar corretamente que f(4) : f(5) é igual a

GABARITO. D

QUESTÃO 05
UECE 2021.1: Em um plano munido com o sistema usual de coordenadas cartesianas, a equação da circunferência que contém os pontos M(0, 2), P(–1, 0) e Q(1, 0) é
A) 2x² – y + 2 = 0.
B) 4x² + y² – 4 = 0.
C) 2x² + y² – y = 0.
D) 2x² + 2y² – 3 y – 2 = 0.
GABARITO. D) 2x² + 2y² – 3 y – 2 = 0.
QUESTÃO 06
UECE 2021.1: Atente para a seguinte lista de números naturais que foi construída seguindo uma lógica estrutural própria: 4, 9, 25, 49, 121, ..........
Considerando essa lógica, é correto dizer que a soma do oitavo com o nono número da lista é igual a
A) 790.
B) 970.
C) 890.
D) 980.
GABARITO. C) 890.
QUESTÃO 07
UECE 2021.1: Seja H um hexágono regular cujo centro é o ponto O. Se X e Y são dois vértices consecutivos de H, o ângulo XÔY é chamado de ângulo central relativo ao lado XY do hexágono.
Se n é a medida, em graus, de cada ângulo central de H e m é a medida, em graus, de cada um dos ângulos internos de H, então, cos²(m+n) + sen²(m–n) é igual a
A) 1,25.
B) 2,00.
C) 1,75.
D) 1,00.
GABARITO. C) 1,75.
QUESTÃO 08
UECE 2021.1: José possui um automóvel que, em uma rodovia, percorre exatamente 12 km com um litro de gasolina. Certo dia, depois de percorrer 252 Km na mesma rodovia, José observou que o ponteiro indicador de combustível que antes marcava  da capacidade do tanque de combustível estava indicando
da capacidade do tanque de combustível estava indicando 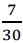
 da capacidade do tanque de combustível estava indicando
da capacidade do tanque de combustível estava indicando 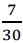
da capacidade do tanque.
Assim, é correto concluir que a capacidade do tanque, em litros, é
A) 40.
B) 35.
C) 45.
D) 30.
GABARITO. B) 35.
QUESTÃO 09
UECE 2021.1: Se definirmos, para cada número natural n,  então, o maior número natural n para o qual bn+1> bn é
então, o maior número natural n para o qual bn+1> bn é
 então, o maior número natural n para o qual bn+1> bn é
então, o maior número natural n para o qual bn+1> bn éA) 3.
B) 5.
C) 4.
D) 6.
GABARITO. C) 4.
QUESTÃO 10
UECE 2021.1: Ao dividirmos o polinômio P(x)=(x–3)³+(x–2)² por (x+1).(x–1) obtemos o resto na forma R(x)=ax+b.
Nestas condições, o valor de a²–b² é igual a
A) –385.
B) –399.
C) –388.
D) –397.
GABARITO. A) –385.
QUESTÃO 11
UECE 2021.1: Em um plano munido do sistema usual de coordenadas cartesianas, a soma das coordenadas dos pontos da reta y=x, cuja distância à reta 2y+x+2=0 é igual a 3, é

GABARITO.
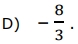
QUESTÃO 12
UECE 2021.1: Seja P(x)=x³+px²+qx–2 onde p e q são números reais tais que P(1+i)=0. Nestas condições, em relação às raízes x1 e x2 da equação x2+qx–p=0, pode-se afirmar corretamente que a soma  é igual a
é igual a
 é igual a
é igual aA) 10.
B) 5.
C) 26.
D) 17.
GABARITO. A) 10.
QUESTÃO 13
UECE 2021.1: No triângulo XYZ, a mediatriz do lado YZ contém a mediana relativa ao vértice X, a medida desta mediana é igual a 2 cm e a medida do lado XY é igual a 3 cm.
Se P é o ponto da reta que contém o lado XY tal que ZP é perpendicular a esta reta, então, a medida, em cm², da área do triângulo PYZ é igual a

GABARITO.
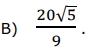
QUESTÃO 14
UECE 2021.1: A medida, em m², da área da região interior à circunferência que circunscreve um triângulo equilátero cuja medida do lado é igual a 12 m é
A) 12 π.
B) 24 π.
C) 36 π.
D) 48 π.
GABARITO. D) 48 π.
QUESTÃO 15
UECE 2021.1: Se n é um número natural, a solução da equação 9 – 2ˣ – 2ˣ⁻¹ – 2ˣ⁻² – .... – 2ˣ⁻ⁿ – ....= 0 é
A) –1 – 2log2(3).
B) –1 + 2log2(3).
C) –2 – log2(3).
D) –2 + log2(3).
GABARITO. B) –1 + 2log2(3).
QUESTÃO 16
UECE 2021.1: Se M é a matriz

e det(M) é o determinante de M, então, para um número inteiro k, todas as soluções x da equação det(M) = 0 são da forma
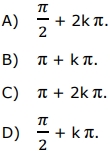
GABARITO. A
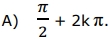
QUESTÃO 17
UECE 2021.1: Se a razão entre as medidas de dois dos ângulos formados pelas diagonais de um retângulo é igual 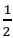 então, é correto afirmar que a razão entre o menor e o maior dos lados do retângulo é
então, é correto afirmar que a razão entre o menor e o maior dos lados do retângulo é
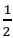 então, é correto afirmar que a razão entre o menor e o maior dos lados do retângulo é
então, é correto afirmar que a razão entre o menor e o maior dos lados do retângulo é
GABARITO. D

QUESTÃO 18
UECE 2021.1: Em um plano, com o sistema usual de coordenadas cartesianas, o gráfico da função quadrática f(x) = ax² + bx + c é a parábola que contém os pontos (0, 9), (2, –5) e (5, 4). Se V(u, v) é o vértice desta parábola, então, a soma u + v é igual a

GABARITO. C

QUESTÃO 19
UECE 2021.1: A quantidade de números inteiros maiores que 2500 formados com quatro dígitos distintos é
A) 3917.
B) 3808.
C) 3528.
D) 3712
GABARITO. B) 3808.
QUESTÃO 20
UECE 2021.1: Considere um poliedro convexo P contido em um cubo cuja medida da aresta é igual a 2 cm. Se P possui exatamente 14 faces e 12 vértices e se os vértices de P são os pontos médios das arestas do cubo, então, é correto afirmar que o volume, em cm³, de P é
Note que seis das faces de P
estão sobre as faces do cubo.

GABARITO.



